How industrial mathematics is changing the way heavy industry makes decisions
As leaders in the application of industrial mathematics (IM), Polymathian has been transforming how heavy industry makes complex decisions. Over the past decade, Polymathian's suite of software products has leveraged IM's power to bring enormous value to customers by solving planning and scheduling problems that are too large and complex to solve manually or with traditional spreadsheets.
But what is industrial mathematics? Fundamentally, IM uses mathematics to solve real-world problems at scale. This requires understanding of the mathematical techniques to use for a given problem, converting real world data into a model, solving the model with the latest computer power, and deploying this in commercially supported, cloud-based software.
The mathematical techniques used to model and solve real-world problems are at the core of IM. These techniques are mathematical optimisation, simulation and advanced analytics. This article, the first in a series, will introduce readers to each of these techniques, why they are used and the types of problems Polymathian is solving for its customers.
Mathematical Optimization
What is mathematical optimisation?
Mathematical optimisation (MO) is a powerful prescriptive analytics technique that enables companies to solve large and complex business problems. According to Polymathian partner Gurobi Optimisation, 85% of Fortune 500 companies use MO in their daily operations to make better business decisions, which results in billions of dollars saved annually.
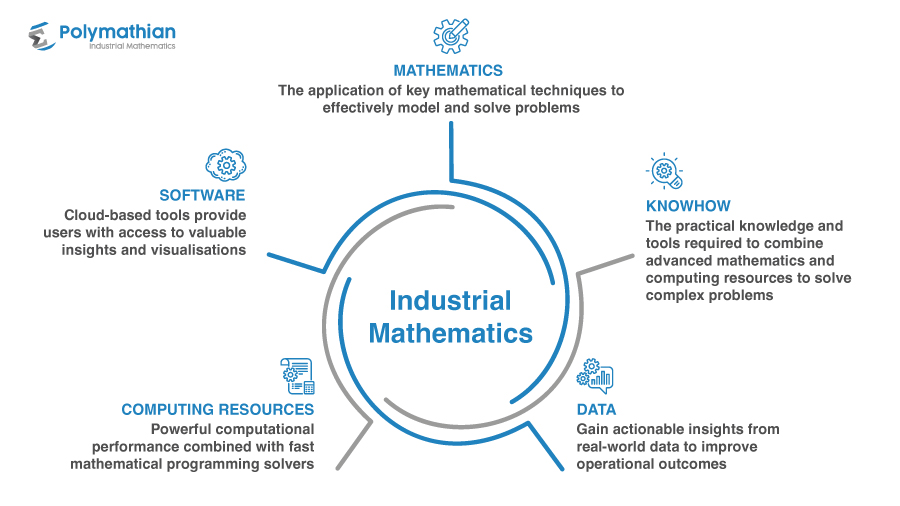
Within the field of MO, Polymathian utilise a technique known as linear programming to build mathematical models of our customer's problems. This model can then be solved to yield provably optimal solutions to the original problem. The ability to identify the quality of a particular solution is the key attribute of linear programming and why it is so widely used.
Through Polymathian's software products, users can build specific scenarios that are comprised of business goals (objectives), decisions (variables) and rules (constraints). Together, these three elements comprise a standalone model which can be solved to maximise or minimise the goal. This process can return a single solution, or a range of solutions which achieve the goal in different ways. By running multiple scenarios, users can gain valuable insights into how the optimal solution changes with respect to the planning rules and decisions.
How is mathematical optimisation used?
Every day, mathematical optimisation is used to plan and execute decisions that impact almost all areas of our lives: the generation and transmission of power to our homes and workplaces; the control of pumps and valves of water pipelines; the routes our smartphones recommend to avoid traffic jams; and the coordination of global multi-modal supply chains essential for modern civilisation.
Planning the material movement and interactions through complex value chains often requires the entire organisation's collaborative efforts, bringing together expertise in production, processing, maintenance, logistics, and marketing. With so many moving parts and operational complexity, plans are often generated in isolation and aggregated together, missing opportunities due to the lack of an integrated planning approach. Many of Polymathian's customers are now using tools like BOLT, our bulk commodity supply chain optimiser, to assist with integrated decision-making that can mathematically find the optimal plan and improve margins by 10%.
Read more.
ORB, Polymathian's mine optimisation software, demonstrates the world's first and most advanced Short Interval Control system for making real-time dispatch decisions in an underground mine. It can dispatch equipment and personnel to priority areas using MO to determine the optimal way to maximise production. By making decisions every minute of every day, ORB has removed the iterative and complex process of manual shift planning and has been able to revolutionise mine production to improve compliance and mine productivity by 20%.
Read more.
Sometimes, however, the tools available within MO cannot accurately describe some complex systems. In these cases, other approaches such as simulation are required.
Simulation
What is simulation?
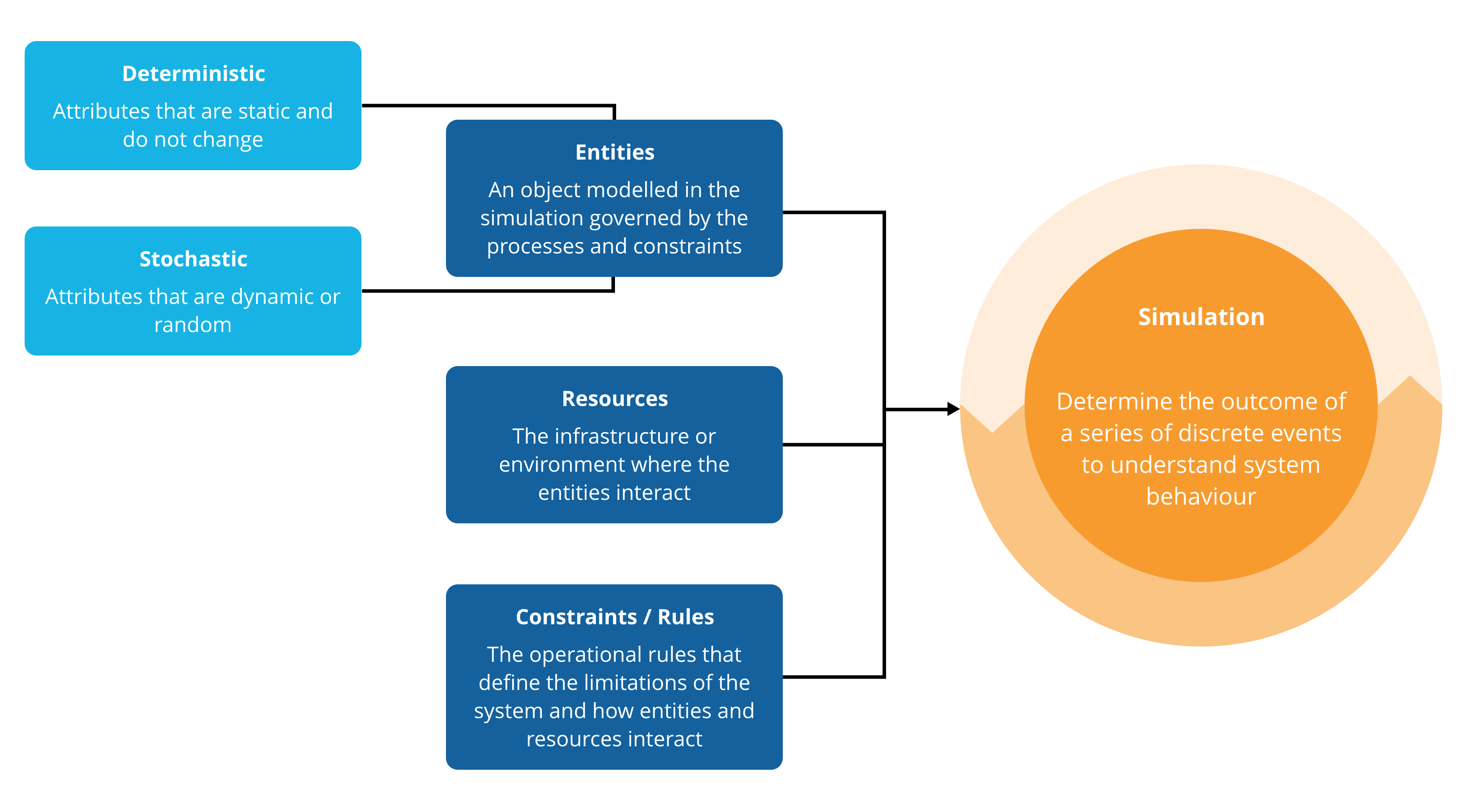
Simulation is a digital model that replicates the operations or processes within a system. It is a tool often used to answer business problems requiring the performance evaluation of a complex operational system. Operational complexity arises from interactions between system entities, task sharing between equipment or constraints related to an event sequence. The performance of these complex systems cannot be calculated using a static model, which is why simulation is used to identify system bottlenecks or the best upgrade options.
System complexity can come in the form of stochastic input data or interactions, complex queuing behaviour, feedback loops, or multiple independent elements within a system. The resulting simulation model allows the user to run virtual scenarios based on the real system, eliminating risk and providing faster results at a much lower cost.
How is simulation used?
Simulation affects a surprisingly large part of everyday life. It provides insights into complex systems to verify or predict future performance, all within a digital environment. Meteorologists use simulation to make weather predictions; traffic engineers establish public transportation timetables and synchronise traffic lights. In industry, simulation is used to analyse risk, plan maintenance, and evaluate capital expenditures.
Simulation provides the ability to test alterations to a system or process in a digital environment without risk. Polymathian deployed a simulation model to take the guesswork out of vessel routing. The customer manages a global supply chain that transports bauxite (the precursor to aluminium) from Australia to domestic and international customers. The complex route planning required a material movement and vessel routing simulation tool, which allowed the customer to understand better how each part of the supply chain affects the other.
Read more.
Polymathian enriches decision making by combining MO with simulation for a major iron ore mine in Western Australia to provide them with a deeper understanding of their conveyor belt network. The customer operates an extensive network of conveyor belts to deliver iron ore from the mines to the processing circuit. The mine relies on the conveyor network to remain productive; therefore, a large inventory of conveyor belt material in varying sizes is warehoused for emergency maintenance. The choice of how much and what type of material to keep in stock is critical because of the raw material costs and the value of operational conveyors. Developing a virtual replica of their system demonstrated how each element of their stocking policy affected their system and how best to manage belt inventory and make CAPEX spending decisions.
Read more.
Advanced Analytics
What is advanced analytics?
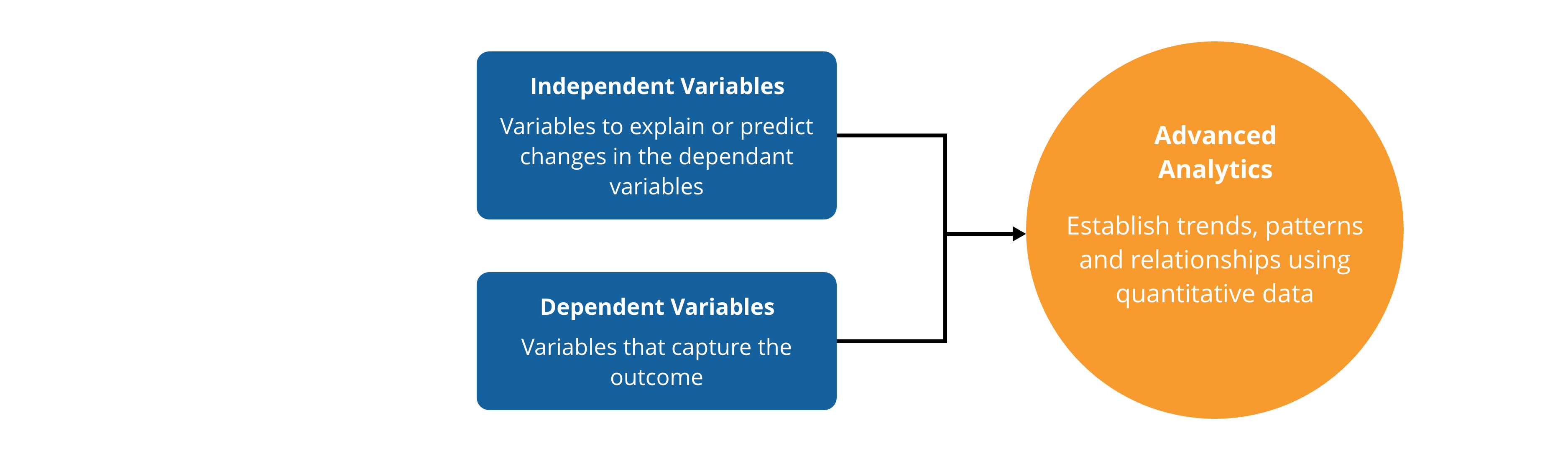
Advanced analytics include techniques such as machine learning or statistical analysis which investigates trends, patterns and relationships using quantitative data. It is used to decide insurance premiums, match product supply to consumer demand, predict unemployment rates, identify supply chain capacity limitations, and even model the spread of COVID-19. Industry has been using advanced analytical techniques for decades to predict future trends, understand supply chains and minimise risk exposure.
Thanks to sensor technology and the 'internet of things' (IoT), businesses today have easy access to vast amounts of data. This is often historical performance data that, through analysis, provides an understanding of the past to make informed decisions to influence future behaviour.
How is advanced analytics used?
Analytics is extensively used in combination with other techniques. The historical data is structured and organised by statisticians or analysts for use in various models depending on desired outcomes.
The key to producing valuable outcomes with analytics is selecting the correct data, as it cannot consider factors outside of the provided data. Statisticians spend a great deal of time selecting the right data to model and analyse to ensure the correct outcomes.
For example, a Polymathian study into the failure of a conveyer belt system revealed that most failures occurred between 11 am and 3 pm (correlation). This data might suggest that it is better to avoid operating during this period of increased risk. However, further analysis of the data showed that this time period is also the busiest of the day, and conveyer failure is more likely due to frequency of use (causation), not the time of day. Therefore, this problem's solution would be to balance the use of the conveyer throughout the day rather than changing operating times.
Machine learning has become extremely prevalent in recent years. This analytical technique requires no underlying model of the real-world system to be developed. Instead, it uses advanced statistical and computational techniques to identify patterns in large volumes of data that can be used to predict future outcomes better.
For one recent customer, Polymathian used statistical analysis and machine learning to improve national sales conversions for Australia's largest enterprises. When machine learning algorithms and exploratory data analysis were applied to enormous volumes of the client's historical data, they were able to gain valuable insights into how effort could be allocated to meet key performance indicators.
Read more.
Conclusion
As illustrated throughout this article, Polymathian utilises three key tools within Industrial Mathematics to solve complex, real-world problems:
- Mathematical optimisation
- Simulation
- Advanced analytics
Each of these techniques, when applied correctly, help solve complex problems in industry. Polymathian work with global organisations to identify how one or more of these can be used together to unlock value and minimise risk.
In future articles in this series, we'll take a deeper dive into each of the mathematical techniques and models, the types of problems they solve and best practices for applying them to your unique business problem.






